The feasible region for #f(x,y)= arcsin(x^2y^25)Ln(x2y1)# is given by #1 le x^2y^25 nn x^2y^25 le 1 nn x 2y 1 > 0# which corresponds to the region plotted in light bluePlease see below Explanation Let's call the function \displaystyle{F} \displaystyle{f{{\left({x}\right)}}}={y}={2}{\ln{{\left({x}^{{2}}{1}\right)}}} The domain9/3/ · \therefore the domain of the function f(x)=\sqrt{\frac{x2}{3x}} is D(f) = 2,3) #7 Find Domain Of A Logarithmic Function From Rule 7 we know that a Logarithmic Function of the form f(x)=\ln \left ( g(x) \right ) is defined when g(x)>0 Example Find the domain of f(x)= \ln (x2) Solution The function f(x)= \ln (x2) is defined when x2>0
Domain And Range And Composition Of Functions
F(x y)=ln(x^2+y^2) domain
F(x y)=ln(x^2+y^2) domain-Domain\f (x)=x^3 domain\f (x)=\ln (x5) domain\f (x)=\frac {1} {x^2} domain\y=\frac {x} {x^26x8} domain\f (x)=\sqrt {x3} domain\f (x)=\cos (2x5) domain\f (x)=\sin (3x) precalculusfunctiondomaincalculator en3/26/18 · Now the domain of the composite map is then $\{(x,y) 1\leq x^{2}y^{2}2\leq 1\}=\{(x,y) 1^{2}\leq x^{2}y^{2}\leq(\sqrt{3})^{2}\}$, the graph is a doughnut of bounded by inner circle with radius $1$ and outer circle with radius $\sqrt{3}$, both circles have center $(0,0)$



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com
And it corresponds to the set of points to the right of, or on, the parabola x = y 2 − 1 (since x ≥ y 2 − 1 ) f ( x, y) = z 2 = z = z (since z ≥ 0) I am going to assume (you should really specify this) that x, y ∈ RThe minimum value of f (x, y) = x 2 y 2 f (x, y) = x 2 y 2 is zero (attained when x = y = 0) x = y = 0) When x = 0, x = 0, the function becomes z = y 2, z = y 2, and when y = 0, y = 0, then the function becomes z = x 2 z = x 2 These are crosssections of the graph, and are parabolas Recall from Introduction to Vectors in Space thatAnswer to Find the domain and range of f(x, y) = ln(3 x^2 y^2) By signing up, you'll get thousands of stepbystep solutions to your homework
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more(c) f(x;y) = ln(x2 y2) Solution x2 y2 > 0 is the domain This consists of all points in the plane except (0;0) This is an open set The range of the function is (1 ;1) Here is a skecth of the level curves f = 1, f = 0, and f = 1Boundary is always given by x= yand the right boundary is always given by the larger value of x for which y= 4x x2 Using the quadratic formula for the equivalent equation x2 4x y= 0, this value is x= 2 p 4 y, so we have ZZ D f(x;y)dA= Z y=3 y=0 Z x=2 p 4 y x=y xdxdy = 1 2 Z y=3 y=0 (2 p 4 y)2 y2 dy = 175 12 8
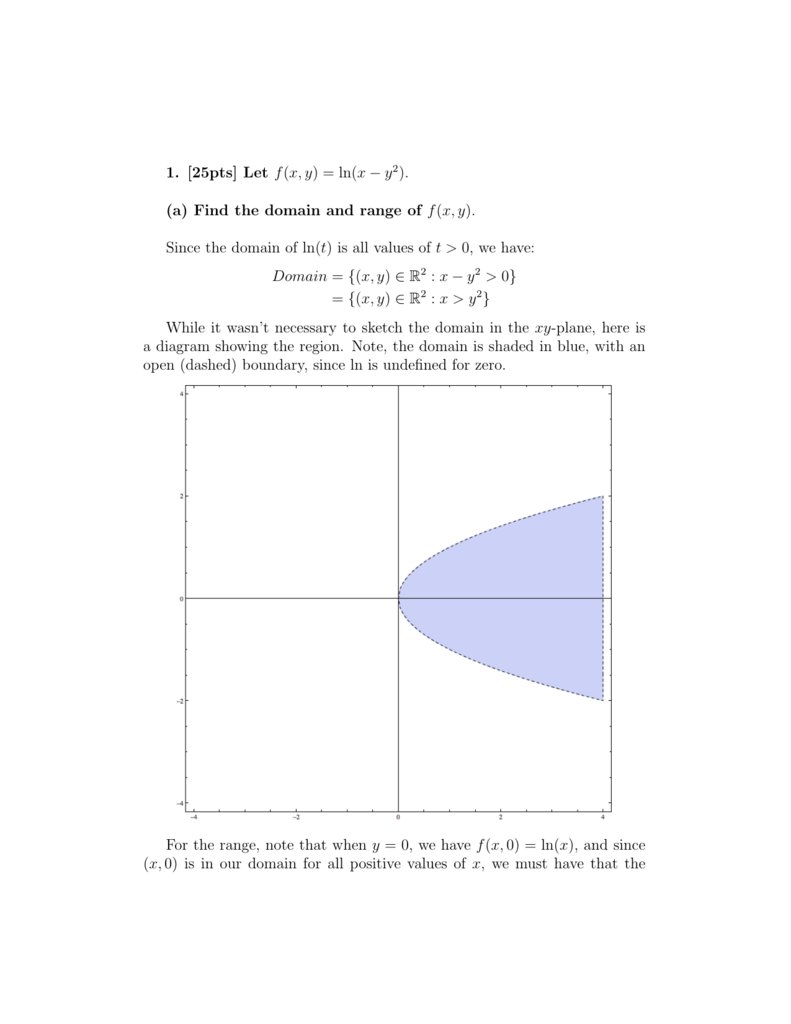
Toms calculus Find the domain of ln(x^2y^24) domains of multivariable functions MasterSkills Tutoring Hire A Tutor in NYC References Helpful Books From Amazon Tom's Math Store About Us Mr Circleman Success Stories Payments and CalendarDomain= f(x;y) 2R2 x y2 >0g = f(x;y) 2R2 x>y2g While it wasn't necessary to sketch the domain in the xyplane, here is a diagram showing the region Note, the domain is shaded in blue, with an open (dashed) boundary, since ln is unde ned for zero For the range, note that when y= 0, we have f(x;0) = ln(x), and since (x;0) is in our domainDefinition 2 The graph of a function f with the two variables x and y is the surface z = f(x,y) formed by the points (x,y,z) in xyzspace with (x,y) in the domain of the function and z = f(x,y) For a point (x,y) in the domain of the function, its value f(x,y) at (x,y) is determined by moving


1 Determine The Domain For The Following Function And Draw The Graph In Xy Plane F X Y Ln X Y 2 8 Marks 2 For Z F X Y E4x2 9y14m Course Hero



Domain And Range And Composition Of Functions
Let z = f(x,y) = ln(x 2 y 2) a) Fine the domain and range of f Domain = x 2 y 2 >0 = Range = ***If this is correct let me know ifthere is a way to work the answer instead of just looking at thegraph and guessing b) Sketch the level curves of f for z = 0, 1, 2 The graph looks like 3 circles placed at the origin with radius =1, e, e 2 respectively *When drawing the graph would thecirclesMore_vert Find and sketch the domain of the function 22 f ( x , y , z ) = ln(16 − 4 x 2 − 4 y 2 z 2 )E y = x Then base e logarithm of x is ln(x) = log e (x) = y The e constant or Euler's number is e ≈ Ln as inverse function of exponential function The natural logarithm function ln(x) is the inverse function of the exponential function e x For x>0, f (f 1 (x)) = e ln(x) = x Or f 1 (f (x)) = ln(e x) = x Natural



6 Ways To Find The Domain Of A Function Wikihow


Local Extrema Of Functions Page 2
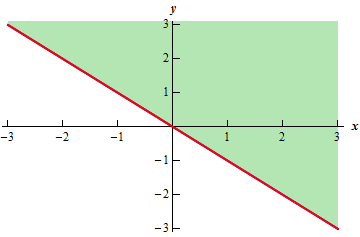
Draw a sketch of the domain as well (a) f(x;y) = p 10 x2 y2 The domain is all points in the xyplane which are on or inside of x2 y2 = 10, the circle with a radius of p 10 centered at the origin (b) f(x;y) = arcsin(2x y) The domain is all points in the xy plane which are between the lines y = 2x 1 and y = 2x 1, including the points on theShare Link y= ln (x^2 3x 2 ) We need to find the domain of the fuction y The domain of y is all x values where the function is defined We know that ln (x^2 3x 2 ) only defined if ( x^2Answer to f(x,y) = 1/ln(4X^2Y^2)Find and sketch the domainI know that the denominator cannot be 0 and ln>0 but I dont know how



Solved 6 A Find The Domain Of The Function F X Y In X Chegg Com


Calculus Iii Functions Of Several Variables
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyF(x,y)=ln(x^2y^2) here we aren't given a particular point (x,y) where we have to check a function's continuity what is to be done if we have to check continuity over the whole domain of the function?آلة حاسبة لمجال دالّة تجد مجال دالّة خطوة بخطوة



Solved Sketch The Domain Of The Function F X Y 12x Chegg Com


5 Derivative Of The Logarithmic Function
Find the Domain and Range y=2^x The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation SetBuilder Notation The range is the set of all valid valuesThis equation into two functions, f(x,y) = p 4− x2 −y2 and f(x,y) = − p 4− x2 −y2, representing the upper and lower hemispheres Each of these is an example of a function with a restricted domain only certain values of x and y make sense (namely, those for which x2 y2 ≤ 4) and the graphs of these functions are limited to a smallDetermine y grafique el dominio de f(x,y)=ln(9x^29y^2) About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new
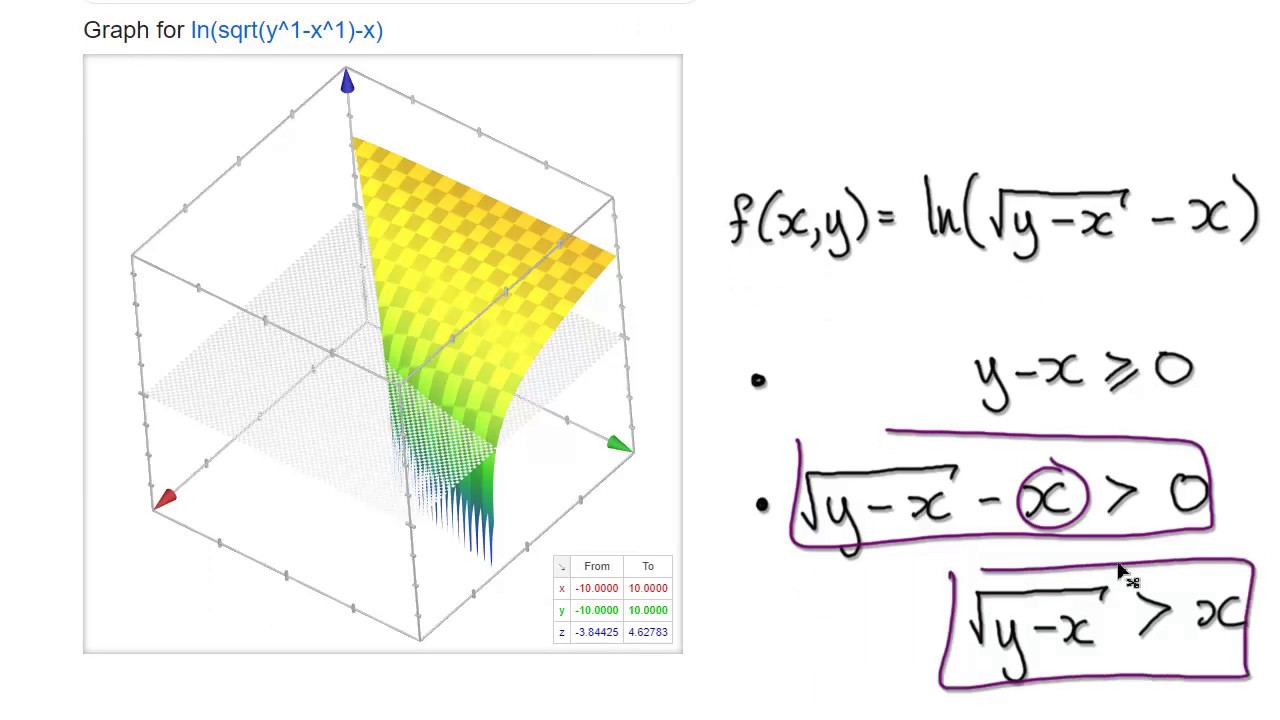


Video 3107 F X Y Ln Sqrt Y X X Multivariable Functions Domain Youtube



Surjective Function Wikipedia
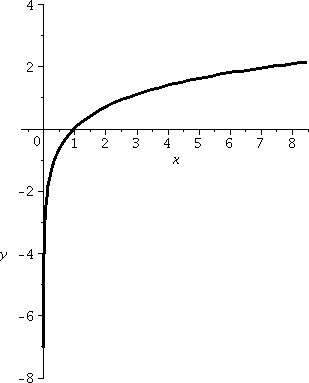
Y > 0g The graph of D is y=−x x y y=x 18 f(x;y) = p x2 y2 1ln(4 x2 y2) Solution For the domain of f we need x2y2 1 0, ie, x2y2 1 and 4 x2 y2 > 0, ie, x2 y2 < 4 So D = f(x;y)j1 x2 y2 < 4g 4 x y 1 5Y x ln(y x) Solution The domain of f is D = f(x;y)jy x and y > xg = f(x;y)j y < x y;4/8/17 · Domain for y=ln(x^2) is x in R but x!=0, in other words (oo,0)uu(0,oo) and range is (oo,oo) We cannot have logarithm of a number less than or equal to zero As x^2 is always positive, only value not permissible is 0


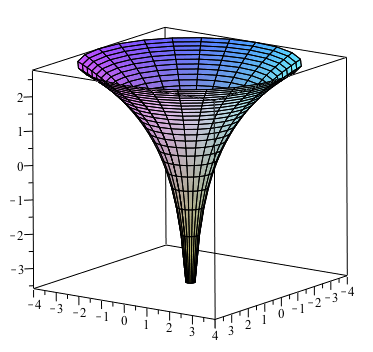
1 25pts Let F X Y Ln X Y 2 A Find The Domain And Range Of F X



Solved Question 22 Find And Sketch The Domain Of The Func Chegg Com
So it's stuff rewriting this says one half and in the square root of X squared So this is going to give us the square root of one half times X So here or domain well, X can take in any row number, so that's from negative Infinity up to infinity on our range is the same thing that's going to be from negative infinity to infinity"}F(x;y) = x2 y2 calculates the height of the paraboloid z = x2 y2 above the point P(x;y) from the two coordinates of P The temperature T of a point on Earth's surface depends on its latitude x and longitude y, expressed by writing T = f(x;y) In this lecture, we de ne functions of more than one independent variable and discuss ways to graph themAssuming both f and square root are being defined for either ℝ>ℝ or for ℂ > ℂ then the domain is all possible numbers of the set If you start out with ℝ then any real number squared is a positive number, and a square root function is defined fo


How Do You Sketch F X Y Ln X 2 Y 2 Socratic



Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube
F (x) = ln (x − 2) f ( x) = ln ( x 2) Set the argument in ln(x−2) ln ( x 2) greater than 0 0 to find where the expression is defined x−2 > 0 x 2 > 0 Add 2 2 to both sides of the inequality x > 2 x > 2 The domain is all values of x x that make the expression defined Interval NotationFind and sketch the domain of the function of f(x;y) = p x2 y2 The inside of a square root must be nonnegative So f(x;y) is defined only if x2 y2 0 In other words, the domain is x2 y2 0 Note that x2 y2 = (x y)(x y) = 0 Therefore the boundary is the union of two diagonal lines passing through the originRegion 2 `{x,y,z2x1>y and x^2 z^2 > 1}` Now, it'd be easy to figure that the region inside of the cylinder looks a lot smaller than the region outside the cylinder However, it all depends on



Find And Sketch The Domain For The Function F X Y Ln X 2 Y 2 100 Study Com



Solved Consider The Function F X Y Ln X 2 Y 2 1 Chegg Com
Find and sketch the domain of the function f(x, y, z) = \sqrt{4 x^2} \sqrt{9 y^2} \sqrt{1 z^2} Join our free STEM summer bootcamps taught by experts Space is limited5/26/ · The domain of functions of two variables, \(z = f\left( {x,y} \right)\), are regions from two dimensional space and consist of all the coordinate pairs, \(\left( {x,y} \right)\), that we could plug into the function and get back a real number {x,y} \right) = \ln \left( {9 {x^2} 9{y^2}} \right)\) Show All Solutions Hide All SolutionsHow to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help support
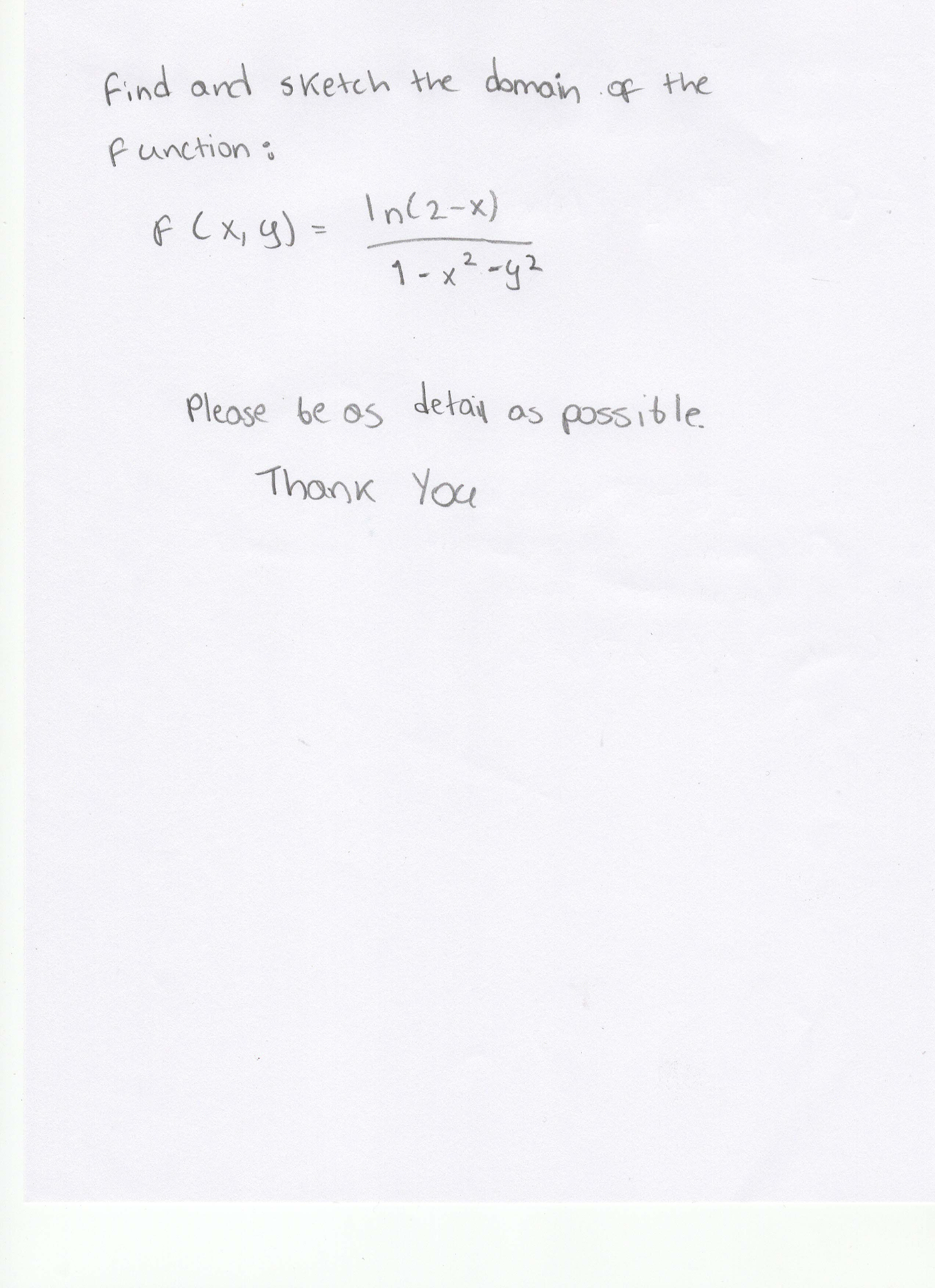


Solved Find And Sketch The Domain Of The Function F X Y Chegg Com


Solved Find And Sketch The Domain For The Function F X Chegg Com
· Answers and Replies You are correct The domain is the number plane excluding only the point (0,0) (the 'origin') The equation x 2 y 2 = 0 can be thought of as a degenerate circle whose center is at (0, 0) and whose radius is 0 In other words, the point (0, 0)(d) f(x;y)=ysinx Solution Step 1 nd critical points f x= ycosx=0 (1) f y=sinx=0 (2) (2) gives x= nˇfor all n2Z, ie integersSubstituting to (1) gives y=0,or y= 0The critical points are (nˇ;0) for all n2ZStep 2 apply second derivative test f xx= −ysinxf yy=0 f xy=cosx At all (nˇ;0), fxx=0,f yy=0,f xy= 1, so D= −19/2/15 · 2 Answers2 1) For the domain, you have the correct set;



How To Find The Domain And Range Of F X Y Ln Xy 2 Youtube



Match The Functions With The Graphs Of Their Domains 1 F X Y Ln 2 X 2 Y 2 F X Y 2 X 2 Y 3 F X Y
0 < 1− x2 − y2 ≤ 1 So the range of f is the set of values of the logarithm in the interval (0,1, which is −∞ < f ≤ 0 Example 162 Find the domain and the range of the function of three variables f(x,y,z) = x2 p z − x2 −y2 Solution The square root is defined only for nonnegativenumbers Therefore, ordered triples (x,y,z(a) f(x;y) = p x2 y2 1 ln(4 x2 y2) The function is de ned for x 2 y 1 0 and 4 x2 y2 0 The domain is D = f(x;y) 2R2j1 x2 y2 < 4g This is an annular region in the xyplane (b) f(x;y) = p x p y p x2 y2 16 The function is de ned for x 0, y 0, and x2 y2 16 0 The domain is D = f(x;y) 2R2jx 0;y 0;x2 y2 16gCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history


If Ln X Y Ln X Ln Y What Are The Values Of X And Y Quora



Find And Sketch The Domain Of The Function F X Y Z Ln 16 4x 2 4y 2 4z 2 Homework Help And Answers Slader
Answer to Given f(x,y)=\lnyx^{2}2, find a The domain b The range c The boundary of the domain d Is the domain open or closed?8/30/19 · Derivative of y = ln u (where u is a function of x) Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types Most often, we need to find the derivative of a logarithm of some function of xFor example, we may need to find the derivative of y = 2 ln (3x 2 − 1) We need the following formula to solve such problemsF(x,y,z) = x2 cosysinz Domains Example f(x,y) = ⇥ ln(x3) ⇤p y 2 x2 4 Cannot have x = ±2 Need x > 3 Need y 2 D f = n (x,y) 2 R2 x > 3 and y 2 o 56 1 FUNCTIONS OF SEVERAL VARIABLES 57 Graphing Functions z = f(x,y) of Two Variables Maple See func2var(121)mw or func2var(121)pdf



Functions Inverses Ppt Download


What Is The Inverse Function Of Ln X Quora



Solved Consider The Function F Defined By F X Y Ln Xy Chegg Com



How To Graph The Domain Of Question 11 Calculus


5 Derivative Of The Logarithmic Function
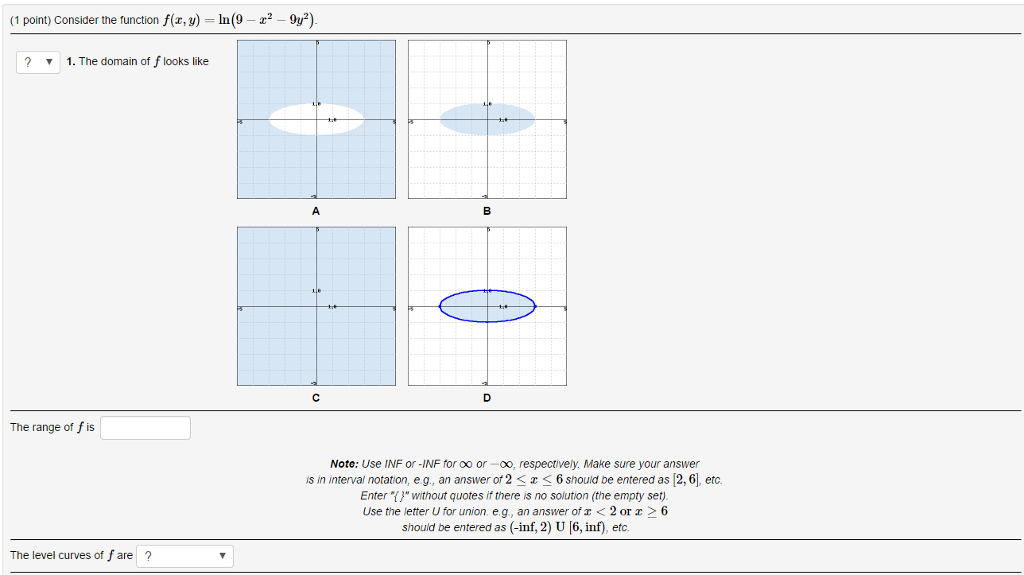


Solved Consider The Function F X Y Ln 9 X 2 9y 2 Chegg Com



Math 148 Exam Iii Practice Problems



Domain And Derivative Of X 2 Ln 1 X 2 Youtube



Solved Consider The Function F X Y In X 2 Y2 1 Chegg Com



Solved Find And Sketch The Domain Of The Function G X Y Chegg Com



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com



Let F X Ln X Y 1 Find And Sketch The Domain Of F What Is The Range Of F Study Com
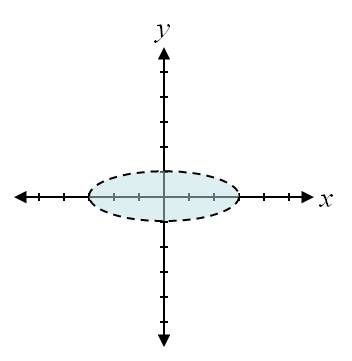


Find And Sketch The Domain Of The Function F X Y Ln 9 X 2 9y 2 Homework Help And Answers Slader



Multivariable Calculus Finding And Sketching The Domain Youtube


Ex 3 Find A Value Of A Directional Derivative F X Y Ln X 2 Y 2 Youtube



Domain Of Natural Logarithm Function F X Ln X 2 Youtube
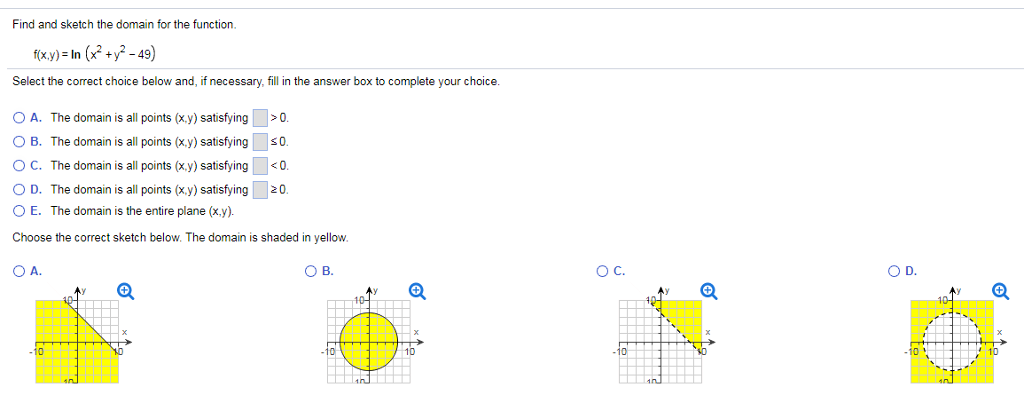


Solved Find And Sketch The Domain For The Function F X Chegg Com



Sketch The Domain Of F Use Solid Lines For Portions Of The Boundary Included In The Domain And Dashed Lines For Portions Not Included F X Y Sqrt



Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com



Find And Sketch The Domain Of The Function F X Y Frac Ln X 2 Y 2 4 Sqrt 4 X 2 Sqrt 4 Y 2 Study Com



Calculating The Derivative Of Ln X 2 Video Lesson Transcript Study Com



F X Ln X 4 Domain Range Graph And Its Inverse Youtube



Find And Sketch The Domain Of The Function F X Y Z Ln 16 4x 2 4y 2 Z 2 Youtube
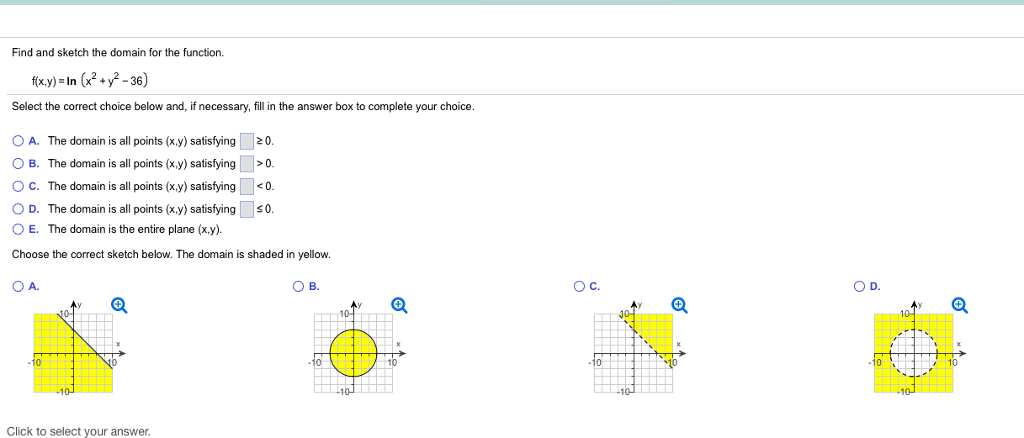


Solved Find The Sketch The Domain For The Function F X Y Chegg Com


Contour Map Of The Function Showing Several Level Curves Physics Forums



Solved Find And Sketch The Domain Of Each Given Function Chegg Com


Injection Surjection Bijection
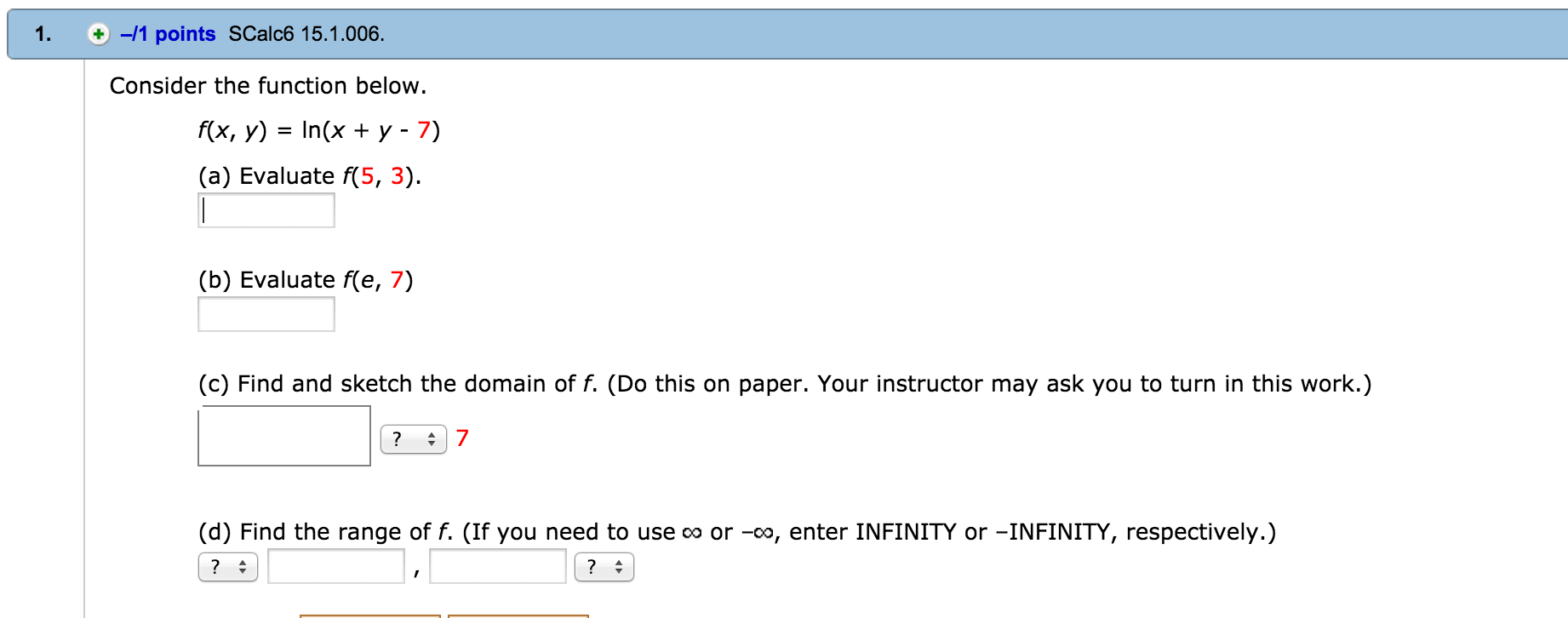


Solved Consider The Function Below F X Y Ln X Y Chegg Com



Domain And Range Of A Function Algebra Socratic


What Is The Domain Of Ln Cosx Quora


If Ln X Y Ln X Ln Y What Are The Values Of X And Y Quora
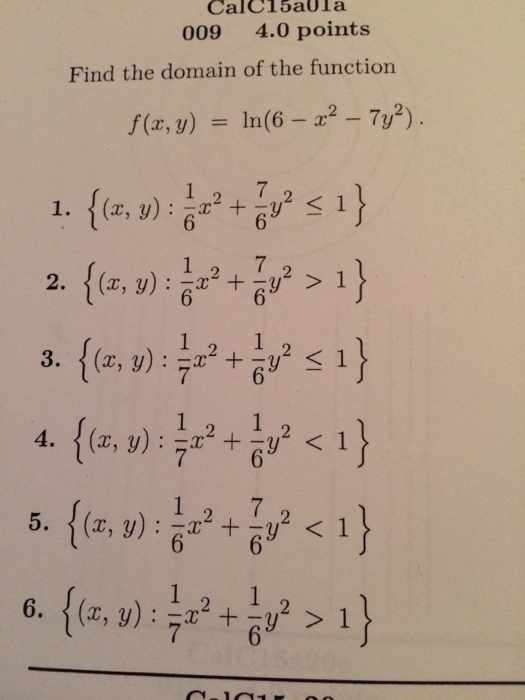


Solved Find The Domain Of The Function F X Y Ln 6 X Chegg Com
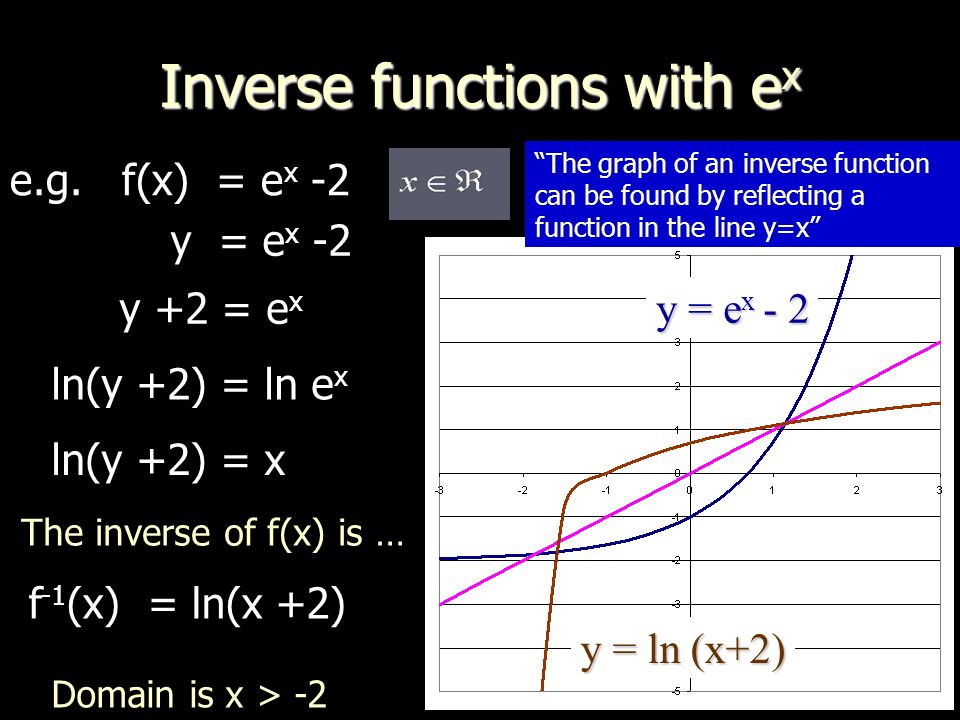


Inverse Functions Recap Of Inverse Of A Function Inverse Functions With E X And Ln X Ppt Download
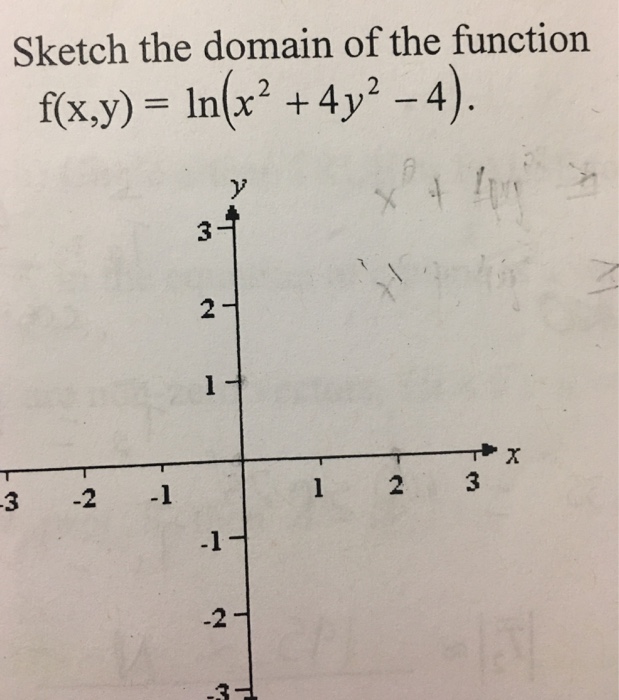


Solved Sketch The Domain Of The Function F X Y Ln X Chegg Com


What Is The Domain Of F X Y Ln Xy Quora



Solved Find And Sketch The Domain For Each Function F X Chegg Com
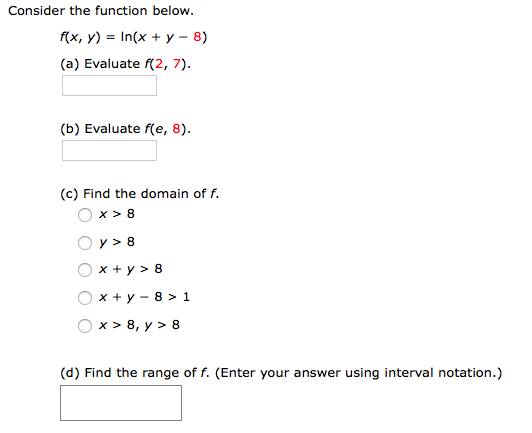


Solved Consider The Function Below F X Y Ln X Y Chegg Com


Functions Of Several Variables Calculus Volume 3



Solved Find The Domain Of The Given Function F X Y 2 L Chegg Com


What Is The Domain Of Ln Cosx Quora


If Ln X Y Ln X Ln Y What Are The Values Of X And Y Quora



Solved For Given Function F X Y Ln X 2 Y 2 81 A Chegg Com


Find And Sketch The Domain Of The Function F X Y Z Ln 16 4x 2 4y 2 4z 2 Homework Help And Answers Slader
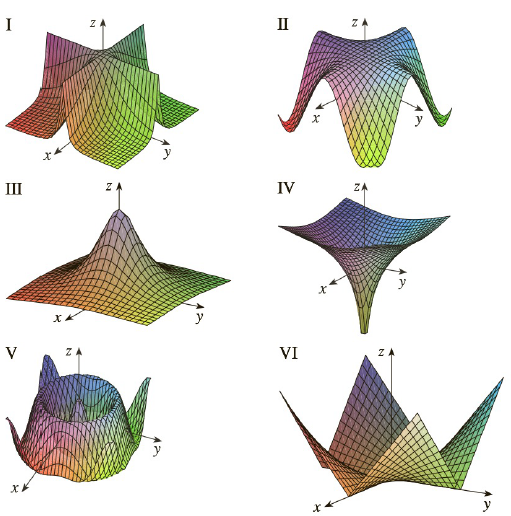


Match The Function With Its Graph Labeled I Vi Give Reasons For Your Choices A F X Y 1 1 X 2 Y 2 B F
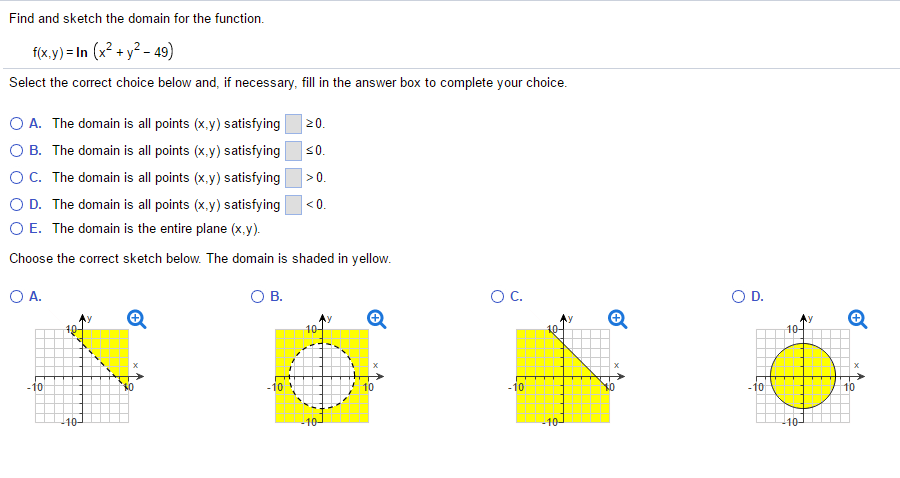


Solved Find And Sketch The Domain For The Function F X Chegg Com



Multivariable Calculus F X Y X Ln Y 2 X Is A Function Of Multiple Variables It S Domain Is A Region In The Xy Plane Ppt Download



Solved Find And Sketch The Domain For Each Functi
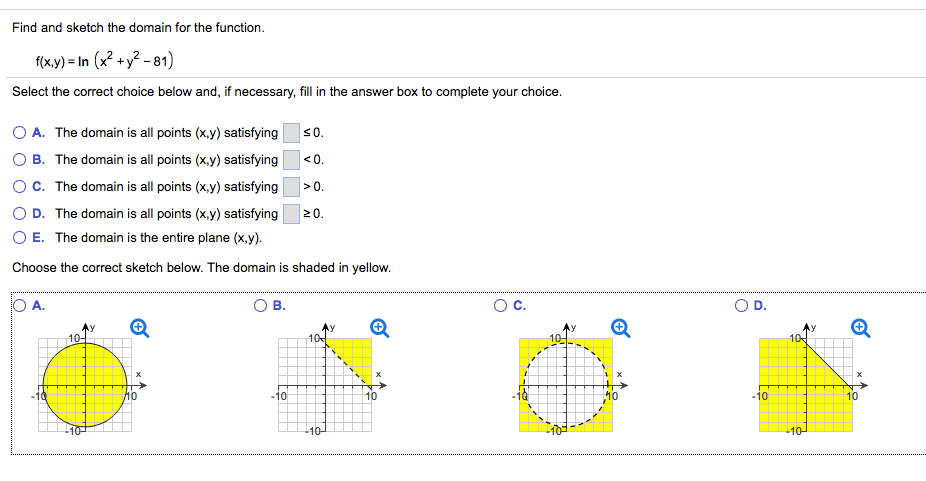


Solved Find And Sketch The Domain For The Function F X Chegg Com



Answered 12 Let G X Y Z X Y Z 10 X Y Bartleby



5 Derivative Of The Logarithmic Function



Multivariable Calculus F X Y X Ln Y 2 X Is A Function Of Multiple Variables It S Domain Is A Region In The Xy Plane Ppt Download



Solved Find And Sketch The Domain Of Each Function A F Chegg Com



If F X Ln X 2 X 2 Rr Rarr Rr And G X X 1 1



14 1 Functions Of Several Variables Mathematics Libretexts



Solved Find And Sketch The Domain Of The Function F X Y Chegg Com
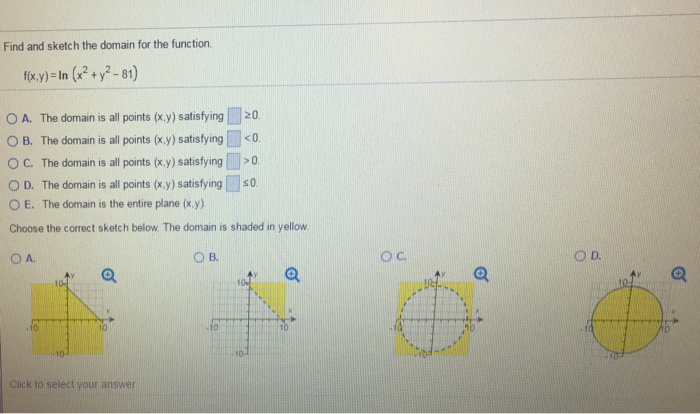


Solved Find And Sketch The Domain For The Function F X Chegg Com


5 Derivative Of The Logarithmic Function


What Is The Minimum Value Of The Function Math F X Y X 2 Y 2 199 Math Over The Real Domain Quora



6 1 The Composition Of Functions F O G Composition Of The Function F With G Is Is Defined By The Equation F O G X F G X The Domain Is The Set Ppt Download



Solved 9 Find The Domain Of F X Y Ln X Y 2 A Y N Chegg Com
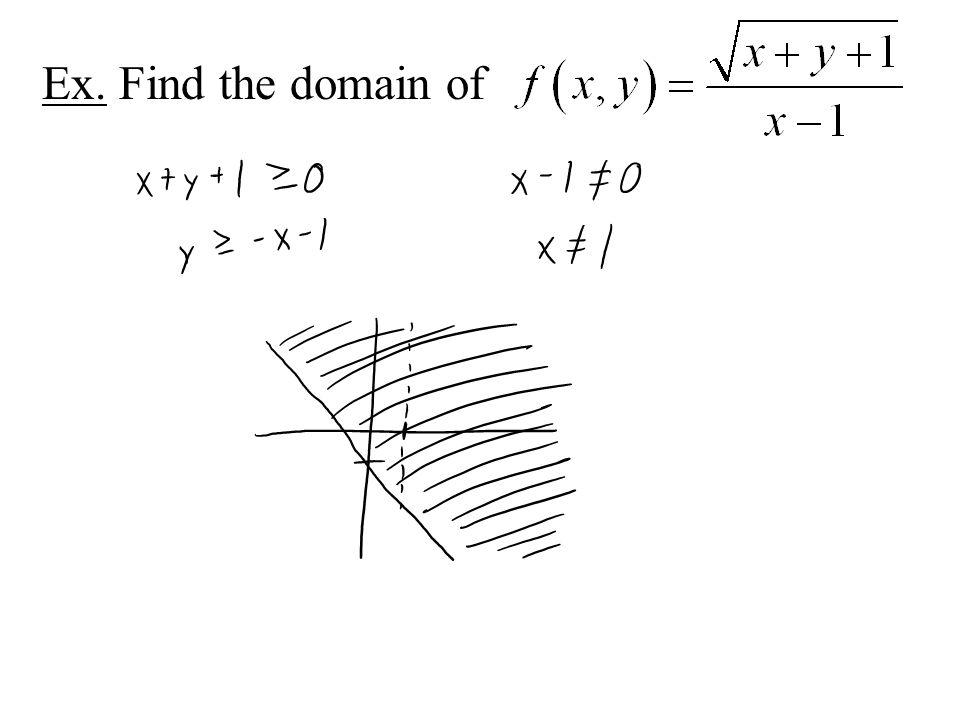


Multivariable Calculus F X Y X Ln Y 2 X Is A Function Of Multiple Variables It S Domain Is A Region In The Xy Plane Ppt Download



Let F X Be Defined In 0 1 Then The Domain Of Definition Of
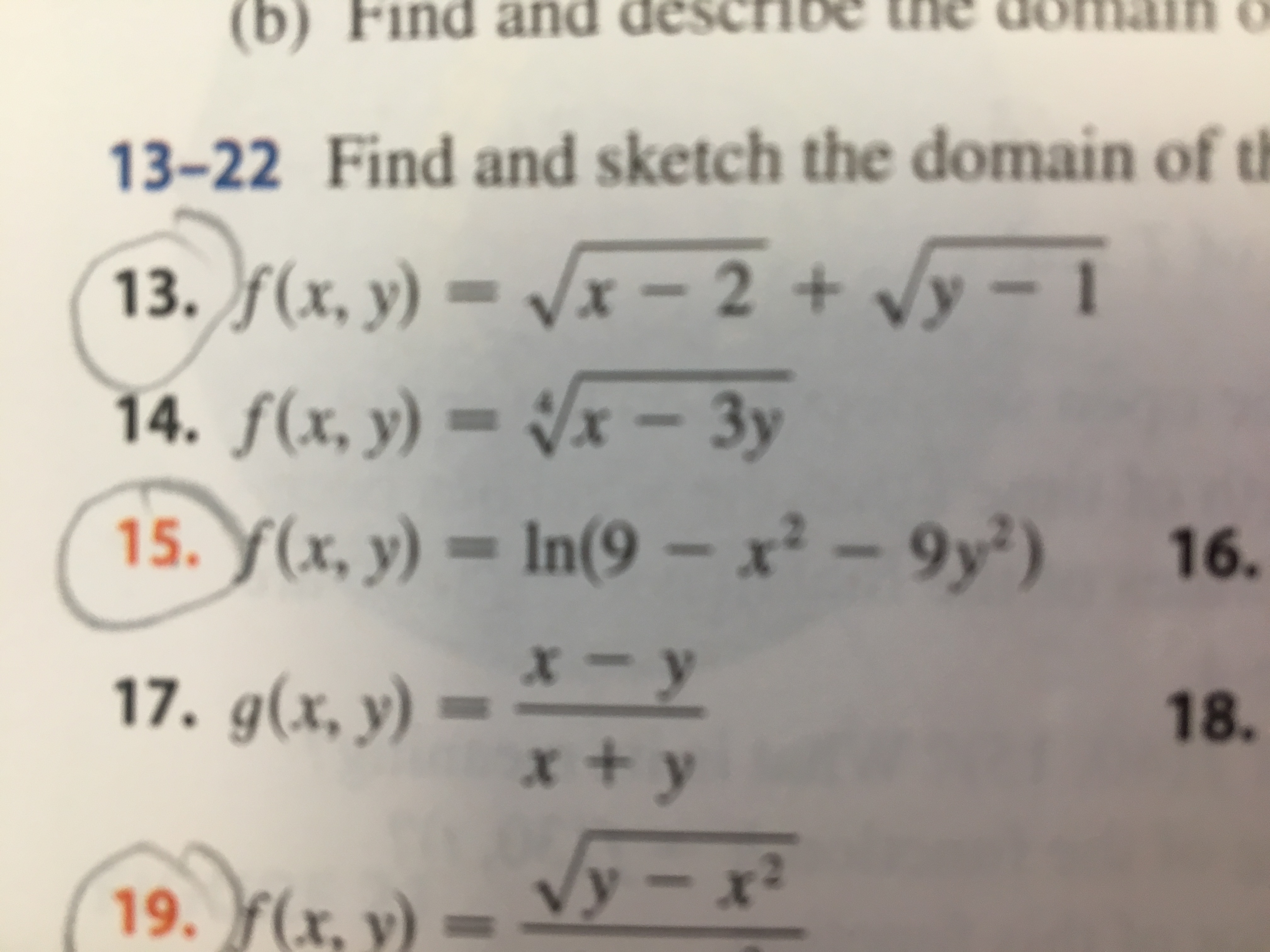


Answered B Find And Describe The Do 13 22 Find Bartleby



Absolute Minima Maxima Entire Domain Video Khan Academy
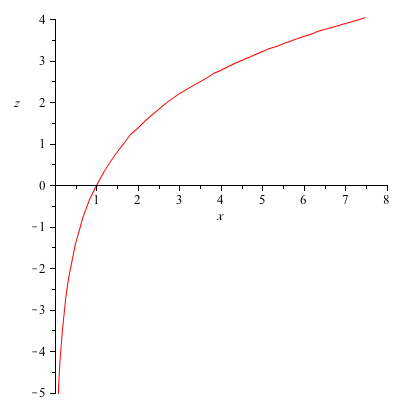


How Do You Sketch F X Y Ln X 2 Y 2 Socratic
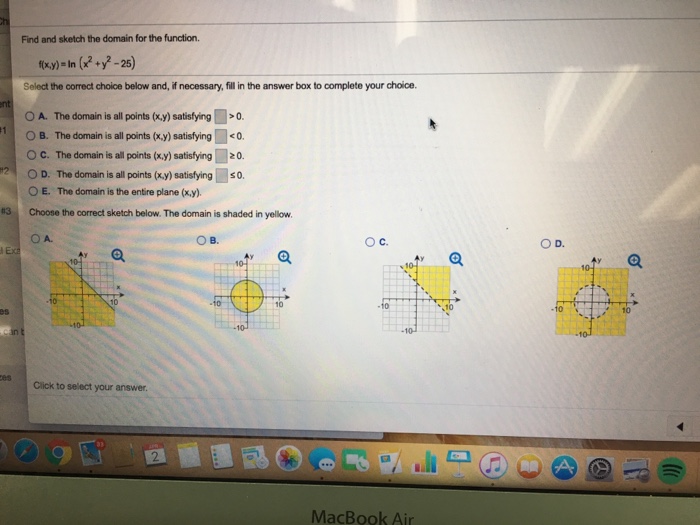


Solved Find And Sketch The Domain For The Function F X Chegg Com
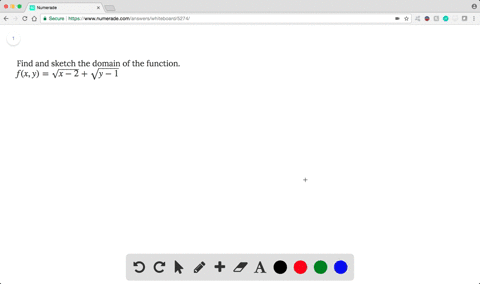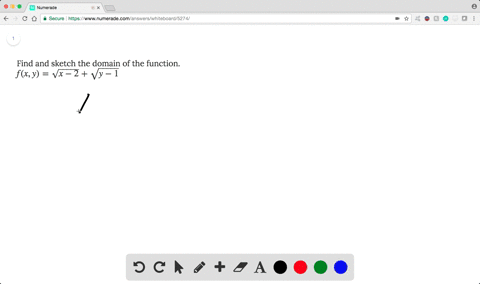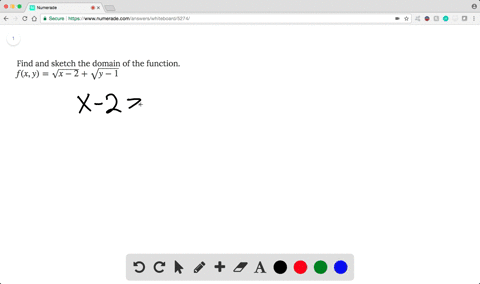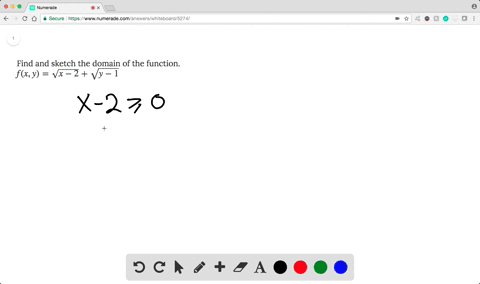


Solved Find And Sketch The Domain Of The Function



0 件のコメント:
コメントを投稿